

The Kepler conjecture postulated an optimal solution for packing spheres hundreds of years before it was proven correct by Thomas Callister Hales. This problem is relevant to a number of scientific disciplines, and has received significant attention. Many of these problems, when the container size is increased in all directions, become equivalent to the problem of packing objects as densely as possible in infinite Euclidean space. In some variants the overlapping (of objects with each other and/or with the boundary of the container) is allowed but should be minimized. More commonly, the aim is to pack all the objects into as few containers as possible.

In some variants, the aim is to find the configuration that packs a single container with the maximal packing density.
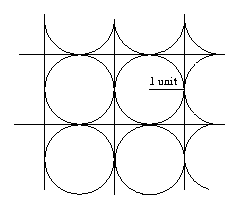
Usually the packing must be without overlaps between goods and other goods or the container walls. The set may contain different objects with their sizes specified, or a single object of a fixed dimension that can be used repeatedly. A set of objects, some or all of which must be packed into one or more containers.Multiple containers may be given depending on the problem. A container, usually a two- or three-dimensional convex region, possibly of infinite size.Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap. Many of these problems can be related to real-life packaging, storage and transportation issues. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers.


 0 kommentar(er)
0 kommentar(er)
